
Треугольник
Серпинского

Список математических достижений и их значимость в математике:
-Решение уравнений в целых числах-
Рассматривается решение уравнений в натуральных, целых или рациональных числах. Серпинский подобрал такие уравнения, решение которых удается получить, не прибегая к средствам теории чисел.
-Числа Серпинского-
В теории чисел нечётное натуральное число k является числом Серпинского, если для любого натурального числа n число k*2 в степени n + 1 является составным.
-Треугольник Серпинского-
Фрактал, один из двумерных аналогов множества Кантора, математическое описание которого опубликовал польский математик Вацлав Серпинский в 1915 году.
Понятия, которые Серпинский вводил во время своих исследований:
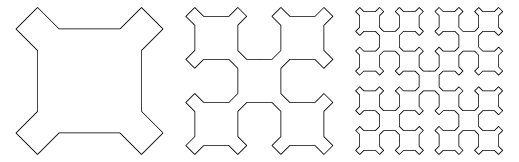
1. Универсальная кривая Серпинского.
Кривые Серпинского — это рекурсивно определённая последовательность непрерывных замкнутых плоских фрактальных кривых, открытых Вацлавом Серпинского.
2. Треугольник Серпинского. Треугольник Серпинского — фрактал, один из двумерных аналогов множества Кантора, математическое описание которого опубликовал польский математик Вацлав Серпинский в 1915 году. Также известен как «салфетка» Серпинского.

3. Ковёр Серпинского.
Фрактал, один из двумерных аналогов множества Кантора, предложенный польским математиком Вацлавом Серпинским в 1916 г.
